6.4 分割类型题

# 6.4 分割类型题

## [279. Perfect Squares](https://leetcode.com/problems/perfect-squares/)

### 题目描述

给定一个正整数，求其最少可以由几个完全平方数相加构成。

### 输入输出样例

输入是给定的正整数，输出也是一个正整数，表示输入的数字最少可以由几个完全平方数相加构成。

```
Input: n = 13
Output: 2
```

在这个样例中，13 的最少构成方法为 4+9。

### 题解

对于分割类型题，动态规划的状态转移方程通常并不依赖相邻的位置，而是依赖于满足分割条件的位置。我们定义一个一维矩阵 dp，其中 dp[i] 表示数字 i 最少可以由几个完全平方数相加构成。在本题中，位置 i 只依赖 $$i - j^2$$ 的位置，如 i - 1、i - 4、i - 9 等等，才能满足完全平方分割的条件。因此 dp[i] 可以取的最小值即为 1+ min(dp[i-1], dp[i-4], dp[i-9] · · · )。注意边界条件的处理。

```py
class Solution:
    def numSquares(self, n: int) -> int:
        dp = [inf] * (n+1)
        dp[0] = 0
        dp[1] = 1
        for i in range(2,n+1):
            for j in range(1,isqrt(i)+1):
                dp[i] = min(dp[i], dp[i-j*j]+1) # 选或者不选
        return dp[n]
```

## [91. Decode Ways](https://leetcode.com/problems/decode-ways/)

### 题目描述

已知字母 A-Z 可以表示成数字 1-26。给定一个数字串，求有多少种不同的字符串等价于这个数字串。

### 输入输出样例

输入是一个由数字组成的字符串，输出是满足条件的解码方式总数。

```
Input: "226"
Output: 3
```

在这个样例中，有三种解码方式：BZ(2 26)、VF(22 6) 或 BBF(2 2 6)。

### 题解

这是一道很经典的动态规划题，难度不大但是十分考验耐心。这是因为只有 1-26 可以表示字母，因此对于一些特殊情况，比如数字 0 或者当相邻两数字大于 26 时，需要有不同的状态转移方程，详见如下代码。

```math
\left\{\begin{array}{l}
f[i]=f[i-1], 1 \leqslant a \leqslant  9 \\
f[i]=f[i-2], 10 \leqslant b \leqslant 26 \\
f[i]=f[i-1]+f[i-2], 1 \leqslant a \leqslant  9,10 \leqslant b \leqslant 26
\end{array}\right.
```

```py
class Solution:
    def numDecodings(self, s: str) -> int:
        n = len(s)
        s = " " + s
        dp = [0] * (n + 1)
        dp[0] = 1
        for i in range(1, n + 1):
            a = ord(s[i]) - ord("0")
            b = (ord(s[i - 1]) - ord("0")) * 10 + ord(s[i]) - ord("0")
            if 1 <= a <= 9:
                dp[i] = dp[i - 1]
            if 10 <= b <= 26:
                dp[i] += dp[i - 2]
        return dp[n]
```

## [139. Word Break](https://leetcode.com/problems/word-break/)

### 题目描述

给定一个字符串和一个字符串集合，求是否存在一种分割方式，使得原字符串分割后的子字符串都可以在集合内找到。

### 输入输出样例

```
Input: s = "applepenapple", wordDict = ["apple", "pen"]
Output: true
```

在这个样例中，字符串可以被分割为 [“apple”,“pen”,“apple”]。

### 题解

类似于完全平方数分割问题，这道题的分割条件由集合内的字符串决定，因此在考虑每个分割位置时，需要遍历字符串集合，以确定当前位置是否可以成功分割。注意对于位置 0，需要初始化值为真。

```py
class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        n = len(s)
        dp = [True] + [False] * n
        for i in range(1,n+1):
            for word in wordDict:
                m = len(word)
                if i >= m and s[i-m:i] == word:
                    dp[i] = dp[i-m]
                if dp[i]:
                    break
        return dp[n]
```

## [1105. Filling Bookcase Shelves](https://leetcode.com/problems/filling-bookcase-shelves/)

### 题目描述

给定一个数组，每个元素代表一本书的厚度和高度。问对于一个固定宽度的书架，如果按照数组中书的顺序从左到右、从上到下摆放，最小总高度是多少。

### 输入输出样例

```
Input: books = [[1,1],[2,3],[2,3],[1,1],[1,1],[1,1],[1,2]], shelfWidth = 4
Output: 6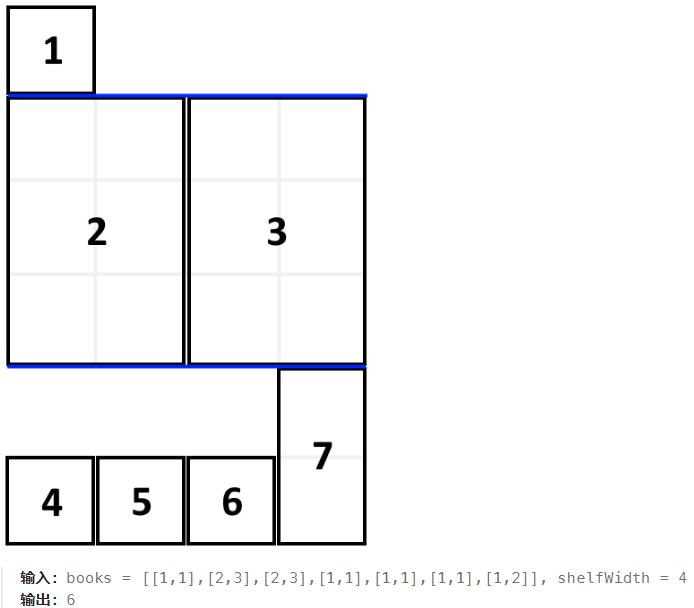
```

![](/media/202503/2025-03-19_124450_7936790.39323935585265435.png)
### 题解

令 dp[i] 表示放置第 i 本书时的最小总高度，则 dp[i] 可以是在第 i-1 本书下面重新放一排，也可以是在满足不超过前一排宽度的情况下放在前一排。

```py
class Solution:
    def minHeightShelves(self, books: List[List[int]], shelfWidth: int) -> int:
        n = len(books)
        dp = [0] * (n+1)
        for i in range(1, n+1):
            width, height = books[i-1]
            # 情况1，放在新的层
            dp[i] = dp[i-1] + height
            # 情况2，放在同一层
            total_width = width
            max_height = height
            for j in range(i-1, 0, -1):
                prev_width, prev_height = books[j-1]
                total_width += prev_width
                if total_width > shelfWidth:
                    break
                max_height = max(max_height, prev_height)
                dp[i] = min(dp[i], dp[j-1] + max_height)
        return dp[n]
```

## [377. Combination Sum IV](https://leetcode.com/problems/combination-sum-iv/)

### 题目描述

给定一个不重复数字的数组和一个目标数，求加起来是目标数的所有排列的总数量。（虽然这道题叫做 Combination Sum，但是不同顺序的组合会被当作不同答案，因此本质上是排列。）

### 输入输出样例

```
Input: nums = [1,2,3], target = 4
Output: 7
```

七种不同的排列为 (1, 1, 1, 1)、(1, 1, 2)、(1, 2, 1)、(1, 3)、(2, 1, 1)、(2, 2) 和 (3, 1)。

### 题解

令 dp[i] 表示加起来和为 i 时，满足条件的排列数量。在内循环中我们可以直接对所有合法数字进行拿取。
```py
class Solution:
    def combinationSum4(self, nums: List[int], target: int) -> int:
        dp = [1] + [0] * target
        for i in range(1, target+1):
            dp[i] = sum(dp[i-num] for num in nums if i >= num)
        return dp[target]
```