第 17 章十大经典排序算法

![](/media/202504/2025-04-23_203150_5764900.2571164881738164.png)

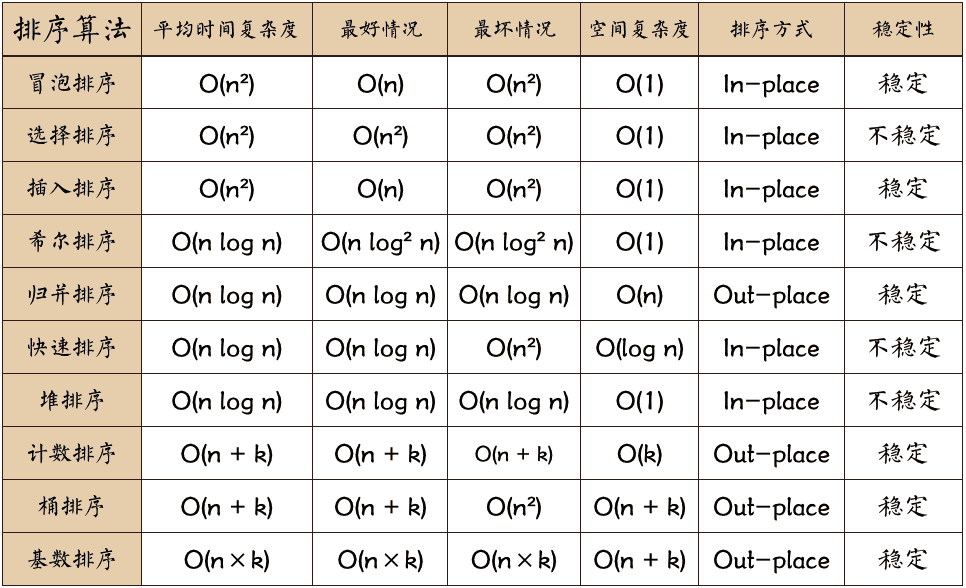## 1. 冒泡排序
冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端
```py
# 冒泡排序，时间复杂度O(n^2)，空间复杂度O(1)
def bubbleSort(nums):
    n = len(nums)
    for i in range(n):
        for j in range(1, n - i):
            if nums[j] < nums[j-1]:
                nums[j], nums[j-1] = nums[j-1], nums[j]
    return nums
```
## 2. 选择排序
首先在未排序序列中找到最小元素，存放到排序序列的起始位置。

再从剩余未排序元素中继续寻找最小元素，然后放到已排序序列的末尾。

重复第二步，直到所有元素均排序完毕。
```py
# 选择排序， 时间复杂度O(n^2)，空间复杂度O(1)
def selectSort(nums:list):
    n = len(nums)
    for i in range(n):
        min_idx = i
        for j in range(i + 1, n):
            if nums[j] < nums[min_idx]:
                min_idx = j
        nums[i], nums[min_idx] = nums[min_idx], nums[i]
    return nums
```
## 3. 插入排序
通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。
从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
```py
# 插入排序，时间复杂度O(n^2)，空间复杂度O(1)
def insertSort(nums):
    # 从第二个元素开始，假设第一个元素已经排好序
    n = len(nums)
    for i in range(1,n):
        key = nums[i] # 当前要插入的元素
        j = i - 1 # 已经排好序的部分
        # 将大于key的元素向后移动一位
        while j >= 0 and key < nums[j]:
            nums[j + 1] = nums[j]
            j -= 1
        nums[j + 1] = key
    return nums
```

## 4. 希尔排序
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行依次直接插入排序。
```py
# 希尔排序，时间复杂度O(nlogn)，空间复杂度O(1)
def shellSort(nums):
    n = len(nums)
    gap = n // 2
    while gap > 0:
        for i in range(gap, n):
            temp = nums[i]
            j = i - gap
            while j >= 0 and nums[j] > temp:
                nums[j+gap] = nums[j]
                j -= gap
            nums[j + gap] = temp
        gap //= 2
    return nums
```
## 5. 归并排序
建立在归并操作上的一种有效的排序算法
分割（Divide）：将数组递归地分成两半，直到每个子数组只有一个元素。
合并（Merge）：将两个有序的子数组合并成一个有序数组。
```py
def mergeSort(nums):
    
    if len(nums)<2:
        return nums
    mid = len(nums)//2
    left, right = nums[0:mid], nums[mid:]
    return merge(mergeSort(left), mergeSort(right))

def merge(left,right):
    res = []
    i = j = 0
    while i < len(left) and j < len(right):
        if left[i] < right[j]:
            res.append(left[i])
            i += 1
        else:
            res.append(right[j])
            j += 1
    res += left[i:]
    res += right[j:]
    return res
```

## 6. 快速排序
从数列中挑出一个元素，称为 "基准"（pivot）;

重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

递归地把小于基准值元素的子数列和大于基准值元素的子数列排序；
```py
def quicksort(nums, low=0, high=None):
    if high is None: high = len(nums)-1
    if low < high:
        pi = partition(nums, low, high)
        quicksort(nums, low, pi-1)
        quicksort(nums, pi+1, high)

def partition(nums, low, high):
    pivot = nums[high]
    i = low - 1
    for j in range(low, high):
        if nums[j] <= pivot:
            i += 1
            nums[i], nums[j] = nums[j], nums[i]
    nums[i+1], nums[high] = nums[high], nums[i+1]
    return i + 
```

## 7. 堆排序
堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。
```py
def heapSort(nums):
    n = len(nums)
    for i in range(n // 2 - 1, -1, -1):
        heapify(nums, n, i)
    for i in range(n - 1, 0, -1):
        nums[i], nums[0] = nums[0], nums[i]
        heapify(nums, i, 0)
    return nums

def heapify(nums, n, i):
    largest = i  
    left = 2 * i + 1  
    right = 2 * i + 2  
    if left < n and nums[left] > nums[largest]:
        largest = left
    if right < n and nums[right] > nums[largest]:
        largest = right
    if largest != i:
        nums[i], nums[largest] = nums[largest], nums[i]
        heapify(nums, n, largest)
```

第 17 章 十大经典排序算法

第 17 章十大经典排序算法